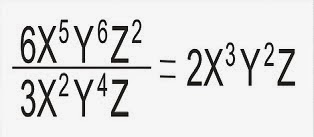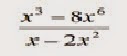DIVISIÓN ALGEBRAICA

La división algebraica es una operación inversa a la multiplicación a través de la cual a partir de dos cantidades llamadas dividendo y divisor se halla una tercera cantidad, llamada cociente.

La división cumple la propiedad distributiva con respecto a la suma y resta por la derecha así:  

y la propiedad de cociente de potencias de igual base

División de Monomios

División de Polinomios por Monomios

Se divide cada uno de los términos del polinomio (dividendo) por el monomio (divisor)

Ejemplos Ilustrativos

Dividir:

1)

                                  

División entre Polinomios

Para dividir un polinomio por otro polinomio, se sugiere el siguiente procedimiento:

- Ordenar los polinomios en forma decreciente.

-Cuando el polinomio dividendo no es completo se reemplazan los correspondientes términos faltantes con variables que tengan coeficientes cero o se deja los espacios, tanto en el dividendo como en el divisor.

- Dividir el primer término del dividendo para el primer término del divisor.

- Cuando los coeficientes del dividendo no son divisibles por los coeficientes del divisor, los cocientes respectivos se escriben en forma fraccionaria

- El primer término del cociente se multiplica por cada uno de los términos del divisor y el producto (con signos opuestos) se resta de los términos semejantes del dividendo, obteniendo así el primer resto parcial.

- El primer término del resto parcial se divide por el primer término del divisor y se obtiene el segundo término del cociente.

- El proceso se repite hasta que el residuo sea cero o de menor grado que el divisor.

Ejemplos Ilustrativos. Dividir:

Cocientes notables

Objetivo: Comprenderás y aplicarás las reglas para obtener el cociente de la diferencia de los cuadrados de dos cantidades entre la suma o la diferencia de las cantidades.

Como en el caso de los productos, existen algunas fracciones que tienen una expresión algebraica específica y que, por su frecuente aparición en los desarrollos algebraicos, es conveniente tener la habilidad de reconocer su estructura y memorizar el resultado a fin de anotar directamente la solución sin necesidad de efectuar la división.

Estas fracciones reciben el nombre de cocientes notables, debido a que se resuelven mediante una división algebraica abreviada que se realiza generalmente de manera visual.

Por supuesto que el resultado se puede obtener realizando la división indicada. Sin embargo,  memorizar y aplicar directamente las reglas que dan la solución, incrementará significativamente la eficiencia en la operatividad algebraica.

Las fracciones más sencillas entre los cocientes notables son:

La diferencia de los cuadrados de dos cantidades dividida por la suma o diferencia de ellas 

Si su cociente se obtiene realizando la división indicada en cada caso, se tiene:

Puesto que las divisiones son exactas, queda:

Estos resultados se pueden recordar con mayor facilidad si se expresan con palabras:

Ø  La diferencia de los cuadrados de dos cantidades dividida por la suma de ellas  es igual a la diferencia de las cantidades.  

Ø  La diferencia de los cuadrados de dos cantidades dividida por la diferencia de las mismas es igual a la suma de las cantidades.
Ejemplo, para dividir:

Lo primero que debe hacerse es observar la estructura de la fracción: el numerador es una diferencia de dos cantidades elevadas a potencias pares, 2 y 6, y el denominador es una suma. El siguiente paso será inspeccionar si el numerador es la diferencia de los cuadrados de las cantidades que aparecen en la suma del denominador. Como

                                  

Se cumple esta condición y se tiene un cociente notable en el que la diferencia de los cuadrados de dos cantidades dividida por la suma de ellas  es igual a la diferencia de las cantidades                      

Para dividir:  

siguiendo el mismo procedimiento. El numerador es una diferencia de términos que tienen potencias pares y cada término de la suma del denominador aparece en el numerador elevado al cuadrado puesto que:

                                

Cociente de la suma o la diferencia de los cubos de dos cantidades entre la suma o la diferencia de las cantidades.

Objetivo: Memorizarás y aplicarás las reglas para obtener el cociente de la suma o la diferencia de los cubos de dos cantidades entre la suma o la diferencia de las cantidades.Además de los dos casos presentados anteriormente, existen otros cocientes que se pueden obtener directamente una vez que se han establecido los resultados generales que les corresponden. Aunque son varias las posibilidades de establecer estos cocientes notables, las reglas para determinarlos resultan ser, en la práctica, tan complicadas como efectuar la división en forma tradicional. Únicamente se presentan dos casos sencillos, que son los correspondientes a los cocientes:

                          

Al dividir el numerador entre el denominador del primer cociente se obtiene:

“La suma de los cubos de dos cantidades dividida por la suma de las cantidades, es igual a la suma de los cuadrados de cada cantidad menos el producto de ambas”.

Por otra parte, la división de la diferencia del cubo de dos cantidades entre la diferencia de las mismas, da el siguiente resultado:

                                     

“La diferencia de los cubos de dos cantidades dividida por la diferencia de las cantidades, es igual a la suma de los cuadrados de cada cantidad más el producto de ambas”

Ejemplos: 1.) Para obtener el cociente de 

Se puede observar que los dos términos del numerador son los cubos de los términos que aparecen sumados en el denominador puesto que y³   es el cubo de y, mientras que 1 es el cubo de 1.

Una vez identificado el caso como un cociente notable, se aplica la regla que dice que el resultado es igual a la suma de los cuadrados de las cantidades menos el producto de ellas  

2.) Para obtener el cociente de

Se observa que los términos del denominador x y 2x²  y los cubos de ellos son x³ y y (2x²)³ = 8x⁶
Entonces, el cociente propuesto es igual a la suma de los cuadrados de las cantidades más el producto de las cantidades:

3.) Para el cociente:

 

como en el segundo término no hay una potencia 3 para suponer a priori que es una diferencia de cubos, conviene hacer primero las operaciones indicadas en el numerador para determinar si corresponde o no, a un cociente notable.

En el numerador existen términos semejantes y, al reducirlos, se obtiene la siguiente expresión: 

Este cociente es inmediato al tomar la regla de la diferencia de cubos de dos cantidades entre la diferencia de las cantidades.

Taller Guiado

Factorización

Halla el factor común en las siguientes expresiones:

1. 4x²y- 8x³y²+ 20x⁴y³

Recuerde que el factor común son los números y las letras que son comunes o sea se repiten en todo la expresión.

¿Cuál es el factor común numérico en esta expresión o sea cuál es el mayor número que divide a todas las cantidades de esta? Ejemplo entre 6, 18 y 15 el factor común es 3 porque es el mayor número que divide a todos.

Nota: El factor común puede estar entre ellos o se puede descomponer en sus factores para hallarlo.

El factor común numérico es ________ 

¿Cuales letras son comunes o aparecen en todas partes de la expresión? De las estas se escoge la de menor exponente.

Las letras que se repiten son:________ Luego el factor común literal es:________ por tanto el factor común es:…………

             Entonces la factorización de 4x²y- 8x³y²+ 20x⁴y³ = ………(……-………+……)

2. 12m²n + 24m³n²-36m⁴n³+ 48m³n⁴ = …….(……… +………… - ……… +………. )
3. 4a³x – 4a²b + 3bm – 3amx  en este ejercicio observa aparentemente que no hay factor común definido ¿Por qué?

Se deben agrupar los términos que tienen términos semejantes de dos en dos para que salga el factor común un ejemplo: En 3xy +6xy³+ 5 +10y² el factor común es 3xy en los dos primeros términos y queda factorizada así 3xy • (1 +2y²)  en los dos últimos términos el factor común es 5 y queda factorizada así   5•(1 + 2y²)  la factorización queda así: 3xy +6xy³+ 5 +10y² = 3xy•(1 +2y²)  + 5•(1 + 2y²) = (1 +2y²) • (3xy+5).

Entonces:

la factorización de  4a³x – 4a²b + 3bm – 3amx = (4a³x – 4a²b) – (3amx - 3bm) =…..(…..- ……) - ….(…. -…..) = (…….  ……….)• (……..  …………)                 

PARA MIS ALUMNOS DE 804

Propiedades de los números Reales  (Continuación)

El conjunto de Números Irracionales: Hasta ahora, tenemos que todo número que se representa por una expansión decimal periódica (finita o infinita) es un número racional, pero cabe hacerse dos preguntas: ¿Existen expansiones decimales que no sean periódicas?, y si existen, ¿son números racionales?

La respuesta de la primera pregunta es afirmativa, como ejemplo, podemos construir el número: 0,1101001000100001000001000000.... Intenta construir alguno.

Los números que se pueden representar por expansiones decimales infinitas no periódicas reciben el nombre de números irracionales. A este conjunto se le denota por I.

Observación 1.1 Por la definición de número racional y la de número irracional se tiene que no existen números que sean racionales e irracionales a la vez, simbólicamente esto se indica de la siguiente manera: Q ∩ I = Ø.

El conjunto de Números Reales: Luego, la unión del conjunto de los números racionales con el conjunto de los números irracionales, recibe el nombre de conjunto de los números reales y se denota con el símbolo R. simbólicamente escribimos: R = Q ∪ I.

1.2. Propiedades de los números reales.

Al combinar los números reales utilizando las operaciones de suma y multiplicación, utilizamos las siguientes propiedades:

Sobre el conjunto R  de los números reales tenemos definidas dos operaciones, la adición y la multiplicación que asignan a cada par   de números reales x,y su suma x+y   y su producto x*y   (que escribiremos abreviadamente como xy  de tal manera que se cumplen las siguientes propiedades básicas:

P.1  CLAUSURATIVA:  R es cerrado para la adición y la multiplicación. Es decir, si  x y y  son números reales, entonces x+y  y x*y son también números reales.

P.2  CONMUTATIVA: La adición y la multiplicación en  son conmutativas. Es decir, si  x y y  son números reales, entonces 

              x+y = y+x                              y                        x*y  = y*x

P.3  ASOCIATIVA: La adición y la multiplicación en R son asociativas. Es decir, si x,y y z  son números reales, entonces ( x+y) + z =  x+(y + z )  y  (x*y)*z = x*(y*z) 

P.4 DISTRIBUTIVA CON RESPECTO A LA ADICIÓN (SUMA): La multiplicación es distributiva, a izquierda y a derecha, con respecto a la adición en R  Es decir, si   x,y y  z  son números reales, entonces: x*(y+z) = x*y+x*z     y  ( x+y)*z= x*z + y*z   

P.5 PROPIEDAD DE IDENTIDAD O MODULATIVA (ELEMENTO NEUTRO)
La propiedad de identidad para la adición dice que existe un número (llamado elemento neutro de la adición) que al ser usado como sumando no cambia el resultado de la suma: x+0 = 0+x = x  
El elemento neutro de la adición es el número CERO.
La propiedad de identidad para la multiplicación dice que existe un número  1  (llamado elemento neutro de la multiplicación) que al ser usado como factor no cambia el resultado de la multiplicación: x*1 = 1*x= x
El elemento neutro de la multiplicación es el número UNO.
P.6 PROPIEDAD DEL INVERSO
La propiedad del inverso aditivo, dice que existe un número que al ser usado como sumando hace que el resultado de la suma sea igual a CERO.  x+(-x) = (-x)+x = 0  
el inverso aditivo para esta suma es el número  
 La propiedad del inverso multiplicativo, dice que existe un número que al ser usado como factor hace que el resultado de la multiplicación sea igual a UNO.        x*1/x = 1/x*x= 1

  

Nomenclatura Algebraica

La Nomenclatura es la manera en la que escribimos las expresiones algebraicas, este concepto nos ayudará más adelante a la hora de determinar cómo resolveremos un problema algebraico.

Expresión Algebraica

Es una combinación de letras, números y signos de operaciones. En álgebra elemental, una expresión puede contener números, variables y operaciones aritméticas. Por convención, éstos generalmente se escriben con los términos con exponente más altos a la izquierda. 

 Ejemplos:  a, 2x, a*(b + c), 2x+y, x²- 5x

Término. Es una expresión algebraica que consta de un solo símbolo o de varios símbolos no separados entre sí por el signo + o - , así por ejemplo: 3a2, xy, -2abc², -xyz

Elementos de un término: Son cuatro: el signo, el coeficiente, la parte literal y el grado, así por ejemplo:

En el caso de 3a² el signo es positivo (cuando un término no va precedido de ningún signo es positivo), el coeficiente es 3, la parte literal es a² y el grado es 2 (segundo grado).

En el caso de -ab²cᶟ el signo es negativo, el coeficiente es 1 (cuando un término no va precedido de ningún coeficiente, el coeficiente es la unidad), la parte literal es ab²cᶟ y el grado de primer grado con relación a la letra a porque el exponente de este factor es l, de segundo grado con relación a la letra b, y de tercer grado con relación a la letra c.

Nota: Para obtener el grado absoluto de un término se suma los exponentes de sus factores literales. En el caso de -2xy²zᶟ el grado absoluto de sexto grado porque la suma de los exponentes de sus factores es 1+2+3=6

Clases de términos

 Término entero: El que no tiene denominador literal, así por ejemplo 7xy²zᶟ.
 Término fraccionario: El que tiene denominador literal, así por ejemplo 3a/b 

 Término racional: El que no tiene radical, como los ejemplos anteriores

 Término irracional: El que tiene radical. Ejemplo  √xy

 Términos homogéneos: Los que tienen el mismo grado absoluto, así por ejemplo 2ab²c⁴ y 5x²y²zᶟ son homogéneos porque ambos son de séptimo grado absoluto

 Términos heterogéneos.  Los que no tienen el mismo grado absoluto

CLASIFICACIÓN DE EXPRESIONES ALGEBRAICAS

Monomio: Es una expresión algebraica que consta de un solo término, así por ejemplo: 7a

Binomio: Es una expresión algebraica que consta de dos términos, así por ejemplo: 3a² – 2a

Trinomio: Es una expresión algebraica que consta de tres términos, así por ejemplo: aᶟ + b - c²

Cuatrinomio: Es una expresión algebraica que consta de cuatro términos, así por ejemplo: xᶟ + 4x² + 2x +1

Nota: En general la expresión algebraica que consta de más de un término (binomio, trinomio, cuatrinomio,...) se llama Polinomio

El grado de un polinomio puede ser absoluto y con relación a una letra

El grado absoluto de un polinomio es el grado de su término de mayor grado. Ejemplo: El polinomio a⁵ - 2a⁴ + a³ – 3a² + a es de quinto grado.

El grado con relación a una letra de un polinomio es el mayor exponente de dicha letra. Ejemplo: El polinomio a⁵ + a²b³ – a⁶b² es de sexto grado con relación a la letra a y de tercer grado con relación a la letra b.